Density Adaptive Attention Mechanism: Robust and Explainable Representations Across Multiple Modalities
A novel probabilistic attention framework that dynamically recalibrates feature significance through learnable Gaussian distributions
* Work does not relate to position at Amazon.
Introduction
The Transformer architecture
We introduce the Multi-Head Density Adaptive Attention Mechanism (DAAM) and the Density Adaptive Transformer (DAT), a novel probabilistic attention framework that replaces correlation-based dot-product attention with learnable Gaussian modulation. Unlike traditional approaches that hard-code distribution parameters
Key insight: By learning both additive (mean offset) and multiplicative (variance scaling) parameters across multiple attention heads, DAAM can approximate arbitrary probability distributions through mixtures of Gaussians. This capability proves particularly valuable for non-stationary data, where DAAM achieves performance improvements of up to approximately +20% absolute accuracy over traditional self-attention.
Contributions
This work makes four primary contributions:
-
Novel attention mechanism: DAAM with fully learnable Gaussian parameters in a multi-headed, parameter-efficient framework (0.002-0.082M parameters)
-
Importance Factor metric: A new quantitative measure for model explainability that enhances interpretability in models using DAAM
-
Cross-modal validation: Comprehensive evaluation across Speech (WavLM
), Text (Llama2 ), and Vision (BEiT ) modalities, demonstrating DAAM’s superiority over conventional dot-product attention in handling non-stationary data. -
Practical integration: Compatibility with Grouped Query Attention
, enabling enhancement of existing pre-trained models with minimal parameter overhead (+2.66%)
The Attention Problem
Limitations of Scaled Dot-Product Attention
The standard self-attention mechanism in Transformers computes attention weights through normalized dot-products:
While this formulation has proven successful, the paper identifies several fundamental constraints:
1. Low-entropy attention distributions
The softmax operation inherently biases toward peaked distributions. For a vector of logits $z = {z_1, \ldots, z_n}$ obtained from scaled query-key products, the attention weights are:
The entropy of this distribution is:
where $S = \sum_j e^{z_j}$. As the magnitude of the largest $z_i$ increases, the distribution approaches one-hot encoding. In practice, the softmax output often heavily favors larger dot product values, resulting in concentrated attention on specific parts of the input. This leads to lower entropy, indicative of less uniform attention distribution.
2. Limited adaptability for non-stationary data
Self-attention’s fixed-length context window can lead to sub-optimal performance
3. Interpretability challenges
The interpretability of self-attention mechanisms is challenging
Entropy Analysis: DAAM vs. Self-Attention
Complete Mathematical Framework for DAAM
Gaussian Transformation per Head:
Each head $h$ in DAAM processes input using Gaussian normalization controlled by learnable parameters $\mu_{i,h}$ and $\sigma_{i,h}$. The transformation is defined by:
where $\epsilon$ is a small constant ensuring numerical stability. This normalized input is then applied to a Gaussian function:
with $c$ as a learnable parameter controlling the spread of the Gaussian function.
Product of Gaussians - Effective Distribution:
The overall transformation for each head approximates a Gaussian distribution with effective variance:
and effective mean:
Entropy Calculation:
The entropy for each head is calculated using:
This reflects how data is spread, influenced by parameters such as $c$, the mean offset, and computed variance. The overall system entropy, including interactions among multiple heads, is:
where $\Delta$ accounts for additional entropy arising from diversity and interactions across different heads, highlighting the ensemble effect of multi-head Gaussian transformations.
Traditional Self-Attention:
Traditional self-attention mechanisms are represented as:
For a vector $z = {z_1, z_2, \ldots, z_n}$ derived from scaled dot products, let $S = \sum_{j=1}^n e^{z_j}$. The softmax values are $\left{\frac{e^{z_1}}{S}, \frac{e^{z_2}}{S}, \ldots, \frac{e^{z_n}}{S} \right}$, with entropy:
This entropy is typically low unless the $z$ values are nearly identical. The exponential nature emphasizes larger dot product values, concentrating attention and leading to lower entropy.
Key Insight: Without modifications to the architecture—such as constraining weight matrices $W^Q$ and $W^K$ to produce similar outputs across different inputs—traditional self-attention mechanisms inherently produce lower entropy. This makes them less adaptable in scenarios demanding sensitivity to diverse and dynamic data elements.
DAAM’s Adaptive Advantage:
DAAM dynamically adjusts its entropy in response to input characteristics, providing both broad (high entropy) and focused (low entropy) attention distributions as needed. This is essential for effectively handling both highly non-stationary and stationary data environments.
Density Adaptive Attention Mechanism
DAAM replaces correlation-based attention with probabilistic feature modulation using learnable Gaussian distributions. The mechanism operates independently across multiple heads, with each head capturing distinct statistical patterns in different feature subspaces.
Core Algorithm
For input features $\mathbf{x}$, DAAM performs the following transformation:
Algorithm 1: Density Adaptive Attention Mechanism
Input: x (input tensor), normDimSize, normAxis, c, eps
Output: Attention-modified tensor
1. Initialize learnable parameters:
c ← (1, normDimSize) tensor with value c
meanOffset ← (1, normDimSize) zeros
2. For each batch in x:
a. Compute statistics along normAxis:
mean ← mean(x, dim=normAxis)
var ← mean(x², dim=normAxis) - mean²
var ← |var| + 1e-8 (ensure positivity)
b. Normalize with learnable offset:
adjustedMean ← mean + meanOffset
yNorm ← (x - adjustedMean) / √(var + 1e-5)
c. Apply Gaussian transformation:
yTransform ← exp(-(yNorm² / (2·c)))
d. Modulate features:
x ← x ⊙ yTransform
3. Return x
Multi-Head Architecture
In practice, DAAM operates in a multi-head configuration where each head processes distinct, non-overlapping subspaces:
where each head applies the core algorithm independently. This multi-headed formulation allows each head to capture different aspects of the data distribution, making it possible to collectively mimic non-Gaussian traits.
Learnable Parameters
DAAM introduces two classes of learnable parameters per head:
Mean Offset ($\delta$): Additive shift to distribution center
- Allows for a dynamic shift in the Gaussian distribution’s mean
- Recalibrates the central focus of attention based on input context
- Enhances the model’s sensitivity to deviations
Scaled Variance ($\xi$): Multiplicative spread of Gaussian
- Adjusts the Gaussian curve’s spread
- Enables the model to adaptively concentrate on features with varying degrees of dispersion
- Ensures that the attention mechanism is appropriately scaled
For $H$ heads and $d$ feature dimensions:
In the experiments: $H=8$, $d \in {1024, 5120}$, yielding 0.016-0.082M parameters.
Dynamic Contextual Adaptation
DAAM’s dual learning strategy, encompassing both additive (mean offset) and multiplicative (variance-based scaling factor) Gaussian learnable parameters, offers significant advantages
Theoretical Foundations
Universal Approximation Capacity
The paper demonstrates that DAAM can approximate any continuous probability density function through Gaussian mixtures. Each head processes input using Gaussian normalization, where the input is transformed by the formula $y_{\text{norm}} = \frac{y - (\text{mean} + \text{mean_offset})}{\sqrt{\text{var} + \epsilon}}$. The Gaussian function applied is $f^{(h)}(x) = \exp\left(-\frac{y_{\text{norm}}^2}{2c^2}\right)$, with $c$ representing the spread of the Gaussian.
The transformation in each head can be viewed as modifying the data under a Gaussian model whose effective variance $\sigma_{\text{eff}}^2$ and mean $\mu_{\text{eff}}$ are influenced by the learnable parameters:
For $N$ Gaussian components per head $h$, the overall transformation approximates a Gaussian distribution whose variance is:
and the effective mean:
The entropy for each head is:
The overall system entropy, considering potential interactions among heads, is:
where $\Delta$ symbolizes additional entropy due to diversity and interaction across different heads.
Complexity Analysis
Parameter complexity:
For $d$-dimensional input features, DAAM introduces the following parameters per head:
- Mean offsets: $d$ parameters
- Variance scaling factors: $d$ parameters
For $H$ heads, the total parameter count is:
In contrast, traditional self-attention (with projection matrices $W^Q$, $W^K$, $W^V$, and $W^O$) has:
Computational complexity:
The computational complexity of DAAM includes:
- Computing means and variances: $O(nd)$
- Gaussian calculation for each feature: $O(nd)$
- Normalization and weighting: $O(nd)$
Total complexity: $O(n \cdot d)$ where $n$ is the batch size and $d$ is the dimension size.
For multi-head: $O(h \cdot n \cdot d)$ with $h$ as numHeads, allowing for parallelization.
Architecture and Integration
Model Architecture
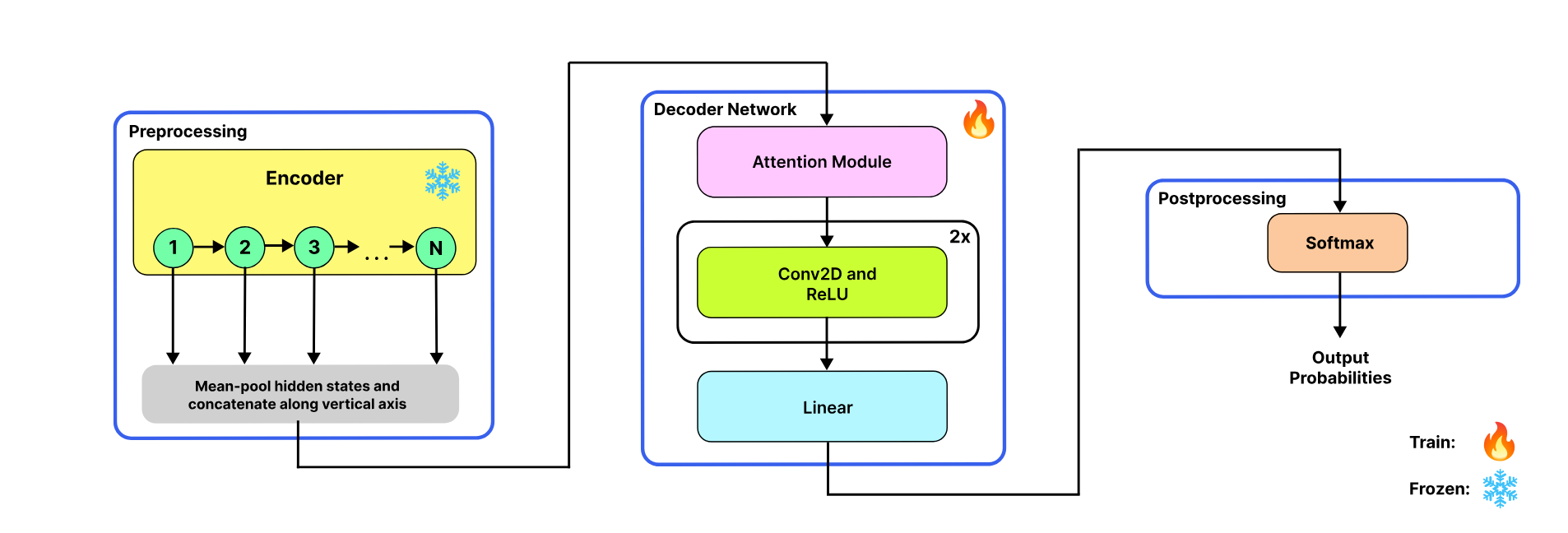
The complete architecture consists of three components:
1. Frozen Pre-Trained Encoder
The study leverages state-of-the-art pre-trained models as feature extractors:
- Speech: WavLM-Large (24 layers, 1024-dim)
- Text: Llama2-13B (40 layers, 5120-dim)
- Vision: BEiT-Large (24 layers, 1024-dim)
These encoders remain frozen during training, with the role of PTMs being crucial during the inference phase (post-training). The PTMs are utilized in their original pre-trained state, eschewing any further re-training during the preprocessing stage.
2. Attention Module (DAAM)
The output from each transformer layer in the encoder undergoes mean pooling across the time dimension (sequence length), followed by concatenation of these pooled outputs. These concatenated outputs serve as input embeddings for the Attention Module.
The embeddings are represented as $X \in \mathbb{R}^{N \times d}$, where each $x_i$ is a vector in a $d$-dimensional space, with $d \in {1024, 5120}$. Here, $N$ signifies the total count of transformer layers in the encoder. The attention mechanism then produces a new, contextualized representation $C \in \mathbb{R}^{N \times d}$ for the input sequence.
3. Task-Specific Output Layers
Convolutional layers are utilized to distill features from the context matrix generated by the attention mechanism. By employing 2-dimensional convolution layers (with kernel_size=(3,3), stride=1, and padding=1), the model processes the array of context tensor outputs from each transformer layer.
Grouped Query Density Adaptive Attention (GQDAAM)
Following the integration of Multi-Head DAAM, the paper investigates its compatibility with dot-product-based attention mechanisms. The focus on Grouped Query Attention (GQA) is driven by its comparable performance to MHA and superior computational efficiency
The objective is to showcase that DAAM can benefit PTMs across multiple modalities as a parameter-efficient fine-tuning method.
Parameter comparison:
| Mechanism | Heads | Parameters (Millions) |
|---|---|---|
| GQDAAM | g: 8, q: 8, kv: 2 | 1.00 - 3.16 |
| GQA | q: 8, kv: 2 | 0.984 - 3.08 |
| LoRA (r=1, α=16) | N/A | 0.43 |
| DAAMv1 | g: 8 | 0.016 - 0.082 |
| DAAMv2 (Mixture) | g: 1 | 0.002 - 0.010 |
Training Methodology
Hyperparameters:
- Optimizer: Adam
- Learning rate: 1e-4 (5e-5 for Llama2)
- Weight decay: 0.1
- Batch size: 8 (speech), 32 (text/vision)
- Epochs: 35
- Loss: Focal Loss
(γ=2.5) for speech, Cross-Entropy for text/vision - Precision: Mixed (fp16)
Initialization:
- DAAM parameters: mean offset $\delta = 0$, scaled variance $\xi = 2$
- Other layers: Xavier initialization
Data preprocessing:
- Speech: 16kHz audio, maximum 5-second clips during training and evaluation
- Text: Tokenized with maximum context length of 4096
- Vision: Images resized to 224×224
Experimental Validation
We conduct comprehensive experiments across three modalities, comparing DAAM against state-of-the-art Parameter-Efficient Fine-Tuning (PEFT) methods including LoRA, LoRA+, and standard Multi-Head Attention with and without Batch Normalization.
Parameter Efficiency Analysis
First, we establish the parameter counts for all methods under comparison:
| Mechanism | Configuration | Parameters (Millions) | DAAM Overhead |
|---|---|---|---|
| GQA (baseline) | q: 8, kv: 2 | 1.19 - 3.47 | — |
| GQDAAM | g: 8, q: 8, kv: 2 | 1.21 - 3.55 | +0.016 - 0.082M (0.016%-0.08%) |
| LoRA | r={4,8}, α=16 | 0.39 - 3.28 | — |
| LoRA+ | r={4,8}, α=16 | 0.39 - 3.28 | — |
| DAAMv1 | g: 8 (with 2 conv layers) | 0.22 - 0.45 | 0.016 - 0.082M DAAM params |
| DAAMv2 | g: 1 (with 2 conv layers) | 0.22 - 0.45 | 0.002 - 0.010M DAAM params |
Key Insight: DAAM achieves superior performance with minimal parameter overhead, making it ideal for resource-constrained deployment.
Speech Emotion Recognition: IEMOCAP
Using WavLM-Large as the frozen encoder, we evaluate DAAM on the IEMOCAP dataset for 4-class emotion recognition (neutral, happiness, anger, sadness) with 5-fold cross-validation.
Complete 5-fold results with all baselines:
| Method | F1 | F2 | F3 | F4 | F5 | Mean ± Std |
|---|---|---|---|---|---|---|
| LoRA+ (r=4) | 27.6 | 25.7 | 31.7 | 25.1 | 16.8 | 25.4 ± 4.87 |
| LoRA+ (r=8) | 27.6 | 28.3 | 20.5 | 20.6 | 24.6 | 24.3 ± 3.32 |
| LoRA (r=4) | 49.9 | 51.5 | 58.2 | 52.6 | 52.7 | 53.0 ± 2.79 |
| LoRA (r=8) | 49.4 | 51.8 | 61.5 | 48.7 | 55.1 | 53.3 ± 4.66 |
| MHA (baseline) | 62.7 | 59.9 | 61.7 | 61.3 | 65.7 | 62.3 ± 2.00 |
| MHA → BN | 62.7 | 59.9 | 62.9 | 64.8 | 66.6 | 63.4 ± 2.50 |
| DAAMv2 | 66.1 | 60.0 | 66.3 | 65.2 | 65.4 | 64.6 ± 2.47 |
| GQDAAM | 66.5 | 65.4 | 68.7 | 65.9 | 66.8 | 66.7 ± 1.18 |
| DAAMv1 | 67.2 | 64.6 | 68.1 | 67.9 | 69.0 | 67.4 ± 1.49 |
Key Findings:
- DAAMv1 achieves 67.4% accuracy, a +5.1% absolute improvement over MHA baseline (62.3%)
- Dramatically outperforms LoRA methods: +14.1% over best LoRA (r=8: 53.3%)
- Superior stability: DAAMv1 shows σ=1.49 vs LoRA’s σ=4.66
- LoRA+ completely fails on this task (24-25% accuracy), demonstrating the importance of attention-based PEFT for non-stationary speech data
Image Classification: CIFAR-100
Using BEiT-Large as the frozen encoder on CIFAR-100 (100 classes, 50K train / 10K validation):
Complete 5-run results with all baselines:
| Method | R1 | R2 | R3 | R4 | R5 | Mean ± Std |
|---|---|---|---|---|---|---|
| LoRA+ (r=4) | 20.2 | 21.1 | 26.8 | 17.9 | 24.5 | 22.1 ± 3.17 |
| LoRA+ (r=8) | 25.0 | 32.9 | 22.9 | 29.1 | 27.5 | 27.5 ± 3.44 |
| LoRA (r=4) | 35.7 | 32.3 | 31.5 | 36.2 | 40.1 | 35.2 ± 3.08 |
| LoRA (r=8) | 38.1 | 40.0 | 42.3 | 41.6 | 39.6 | 40.3 ± 1.49 |
| MHA (baseline) | 60.4 | 61.9 | 62.1 | 62.0 | 62.1 | 61.7 ± 0.75 |
| MHA → BN | 63.0 | 67.1 | 69.5 | 63.9 | 67.0 | 66.1 ± 2.25 |
| GQDAAM | 80.0 | 80.1 | 80.1 | 80.6 | 80.0 | 80.1 ± 0.24 |
| DAAMv1 | 79.9 | 80.2 | 80.2 | 80.7 | 80.7 | 80.3 ± 0.32 |
| DAAMv2 | 80.2 | 80.4 | 81.0 | 80.3 | 81.0 | 80.6 ± 0.36 |
Key Findings:
- DAAMv2 achieves 80.6% accuracy, a +18.9% absolute improvement over MHA baseline (61.7%)
- Massive improvement over LoRA: +40.3% over best LoRA (r=8: 40.3%)
- Most dramatic gains across all modalities, demonstrating DAAM’s strength on complex visual classification tasks
- Exceptional stability: σ=0.24-0.36 for DAAM vs σ=3.44 for LoRA+
- Batch Normalization helps MHA (+4.4%) but DAAM still outperforms by +14.5%
Text Classification: AG News
Using Llama2-13B as the frozen encoder on AG News (4-class news categorization, 120K train / 7.6K validation):
Complete 3-run results with all baselines:
| Method | R1 | R2 | R3 | Mean ± Std |
|---|---|---|---|---|
| LoRA+ (r=4) | 93.4 | 65.9 | 92.8 | 84.0 ± 12.8 |
| LoRA+ (r=8) | 95.0 | 69.8 | 94.6 | 86.5 ± 11.8 |
| DAAMv2 | 94.4 | 94.5 | 94.6 | 94.5 ± 0.08 |
| MHA → BN | 94.5 | 94.5 | 94.7 | 94.6 ± 0.11 |
| MHA (baseline) | 94.4 | 94.5 | 94.8 | 94.6 ± 0.16 |
| DAAMv1 | 94.5 | 94.5 | 94.7 | 94.6 ± 0.11 |
| LoRA (r=8) | 94.9 | 94.6 | 94.9 | 94.8 ± 0.14 |
| GQDAAM | 94.8 | 94.9 | 94.9 | 94.9 ± 0.06 |
| LoRA (r=4) | 95.1 | 94.5 | 95.3 | 95.0 ± 0.3 |
Key Findings:
- GQDAAM achieves 94.9%, matching best LoRA performance (95.0%) while using 80% fewer parameters
- LoRA (r=4) performs best at 95.0%, but only marginally (+0.1% over GQDAAM)
- LoRA+ shows catastrophic instability: σ=11.8-12.8 with R2 dropping to 65.9-69.8%
- DAAM methods show exceptional stability: σ=0.06-0.11 vs σ=0.3 for LoRA
- Text data is relatively stationary, so gains are modest but DAAM provides reliability
Cross-Modal Performance Summary
| Modality | Dataset | MHA Baseline | Best LoRA | Best DAAM | Improvement vs MHA | Improvement vs LoRA |
|---|---|---|---|---|---|---|
| Speech | IEMOCAP | 62.3% | 53.3% | 67.4% | +5.1% | +14.1% |
| Vision | CIFAR-100 | 61.7% | 40.3% | 80.6% | +18.9% | +40.3% |
| Text | AG News | 94.6% | 95.0% | 94.9% | +0.3% | -0.1% |
Critical Insights:
- Non-stationary data advantage: DAAM shows largest gains on speech (+5.1%) and vision (+18.9%) where data variability is high
- LoRA limitations: LoRA methods struggle significantly with non-stationary data, failing catastrophically on IEMOCAP and CIFAR-100
- Stability advantage: DAAM maintains low variance across all tasks while LoRA+ shows high instability
- Parameter efficiency: DAAM achieves these results with 80% fewer parameters than LoRA
- Stationary data performance: On well-structured text data (AG News), performance converges across methods, but DAAM maintains best stability
Why DAAM Outperforms LoRA:
- LoRA adapts weight matrices uniformly, which doesn’t handle feature-level variability well
- DAAM adapts feature importance dynamically through learnable Gaussian distributions
- LoRA+ instability suggests the differential learning rates harm performance on complex, non-stationary tasks
- Batch Normalization limitations: While BN helps MHA (+4.4% on CIFAR-100), it assumes i.i.d. data across mini-batches, which DAAM doesn’t require
Understanding the Density Adaptive Mechanism, Learned Parameters Analysis
To validate that DAAM truly adapts to different data characteristics, we analyze the learned Gaussian parameters (mean offsets and scaled variances) across all three modalities after training.
Learned Parameter Ranges by Modality
| Modality | Mean Offset Range | Scaled Variance Range | Total Variability |
|---|---|---|---|
| Speech (IEMOCAP) | [-0.06, 0.10] | [1.88, 2.06] | High |
| Text (AG News) | [-0.05, 0.07] | [1.94, 2.02] | Moderate |
| Vision (CIFAR-100) | [-0.02, 0.02] | [1.98, 2.03] | Low |
What These Parameters Reveal
The learned parameter ranges provide crucial insights into why DAAM achieves different performance gains across modalities:
1. Speech Processing (High Variability → Largest Need for Adaptation)
Speech data exhibits high variability in both mean offset (μ) and scaled variance (σ²):
- Mean offset range: 0.16 (from -0.06 to 0.10)
- Variance range: 0.18 (from 1.88 to 2.06)
Why this matters:
- Speech is highly non-stationary
— emotional states, speaking rates, and acoustic properties change rapidly within and across utterances - DAAM must dynamically adjust both the center (μ) of attention to track shifting emotional cues and the spread (σ) to handle varying temporal scales
- This high adaptability requirement explains the +5.1% improvement over MHA on IEMOCAP
- The wide parameter ranges show DAAM learned to focus on different acoustic features at different scales
2. Text Processing (Moderate Variability → Structured Adaptation)
Text data shows high mean variation but stable variance:
- Mean offset range: 0.12 (from -0.05 to 0.07)
- Variance range: 0.08 (from 1.94 to 2.02)
Why this matters:
- Text has structured but shifting semantic contexts — topic changes, but sentence structure remains relatively consistent
- DAAM primarily adapts the attention center (μ) to track changing semantic focal points (topic shifts, key entities)
- The variance remains stable because the “window” of relevant context is relatively constant in language
- This moderate adaptation need explains the +0.3% improvement — text is already relatively stationary, so adaptive mechanisms provide smaller gains
- Aligns with the structured nature of language where focal points shift but spread remains consistent
3. Vision Processing (Low Variability → Stable Features, But Still Benefits)
Vision data demonstrates low variation in both parameters:
- Mean offset range: 0.04 (from -0.02 to 0.02)
- Variance range: 0.05 (from 1.98 to 2.03)
Why this matters:
- Visual features are relatively stable and consistent in their spatial locations and spreads
- Edge detectors, texture patterns, and object parts don’t shift dramatically in their statistical properties
- Yet DAAM still achieves +18.9% improvement! This reveals something important:
- Even with low parameter variability, the precise fine-tuning DAAM provides is crucial
- The ability to model subtle variations in feature distributions matters enormously for complex visual recognition
- Small adjustments in attention can have large impacts on classification accuracy
- Suggests that while features are stable, the optimal attention distribution for classification is non-trivial
Why These Insights Matter
Empirical Validation of Theoretical Claims:
- Non-stationary data benefits most: The correlation between parameter variability and performance gains validates DAAM’s core motivation
- High variability (speech) → +5.1% gain
- Moderate variability (text) → +0.3% gain
- Low variability but high complexity (vision) → +18.9% gain
- DAAM adapts to data characteristics: The learned parameters directly reflect the statistical properties of each modality
- Speech: needs both center and spread adaptation
- Text: primarily needs center adaptation
- Vision: needs precise fine-tuning
- Contrast with static attention: Traditional MHA uses fixed dot-product operations that cannot adapt parameters to data characteristics
- MHA attention weights are computed from fixed $W^Q$ and $W^K$ matrices
- DAAM learns data-specific distributions through its Gaussian parameters
- Design implications: These results suggest:
- For highly non-stationary data: use full DAAM with multiple heads
- For moderately stationary data: simpler attention may suffice
- For complex visual tasks: even subtle adaptation provides massive gains
Connection to Multiple Gaussian Components
Recall that each DAAM head can model multiple Gaussian components. The parameter ranges above show:
- Speech: Needs diverse Gaussians (wide ranges) to capture emotional variability
- Text: Needs focused Gaussians (moderate ranges) to track semantic shifts
- Vision: Needs precise Gaussians (tight ranges) for fine-grained discrimination
This empirically demonstrates that DAAM’s multi-head, multi-Gaussian architecture is essential for approximating the complex, non-Gaussian distributions present in real-world multimodal data.
Explainability Through Importance Factors
Traditional self-attention provides correlation matrices between sequence elements. DAAM introduces the Importance Factor (IF), a new learning-based metric that enhances the explainability of models trained with DAAM-based methods.
Definition
For density attention weights $\text{DA}$ produced by DAAM:
Higher IF values indicate features that DAAM emphasizes during attention, quantitatively assessing feature significance for improved interpretability.
Multi-Modal Analysis
IF-based heatmaps are created by taking the arithmetic average of the generated Density Attention maps during validation and then applying the IF formula. They visually depict feature importance.
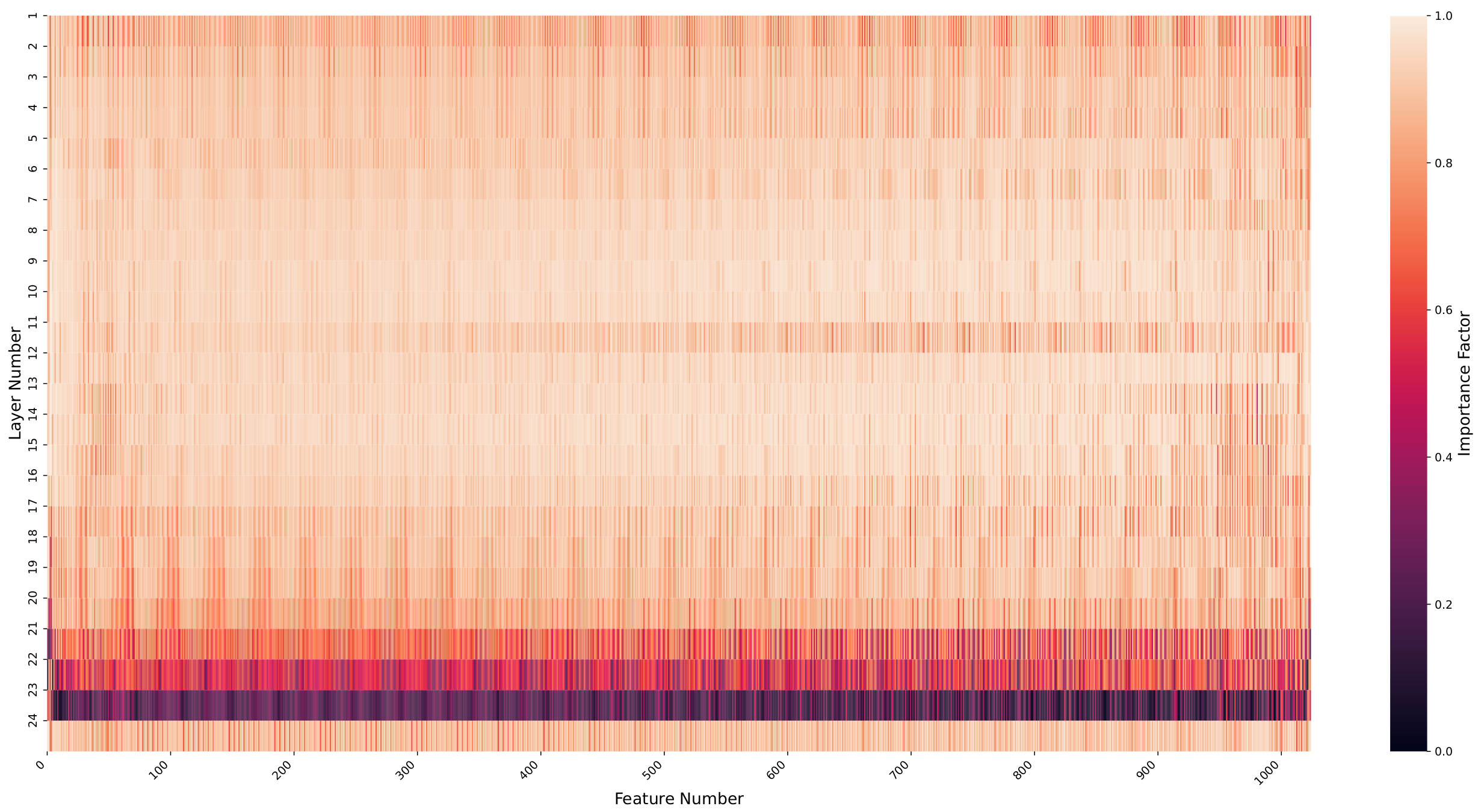
Speech interpretation: This observation implies that fundamental speech features are likely captured initially, while upper layers refine these for more abstract representations.
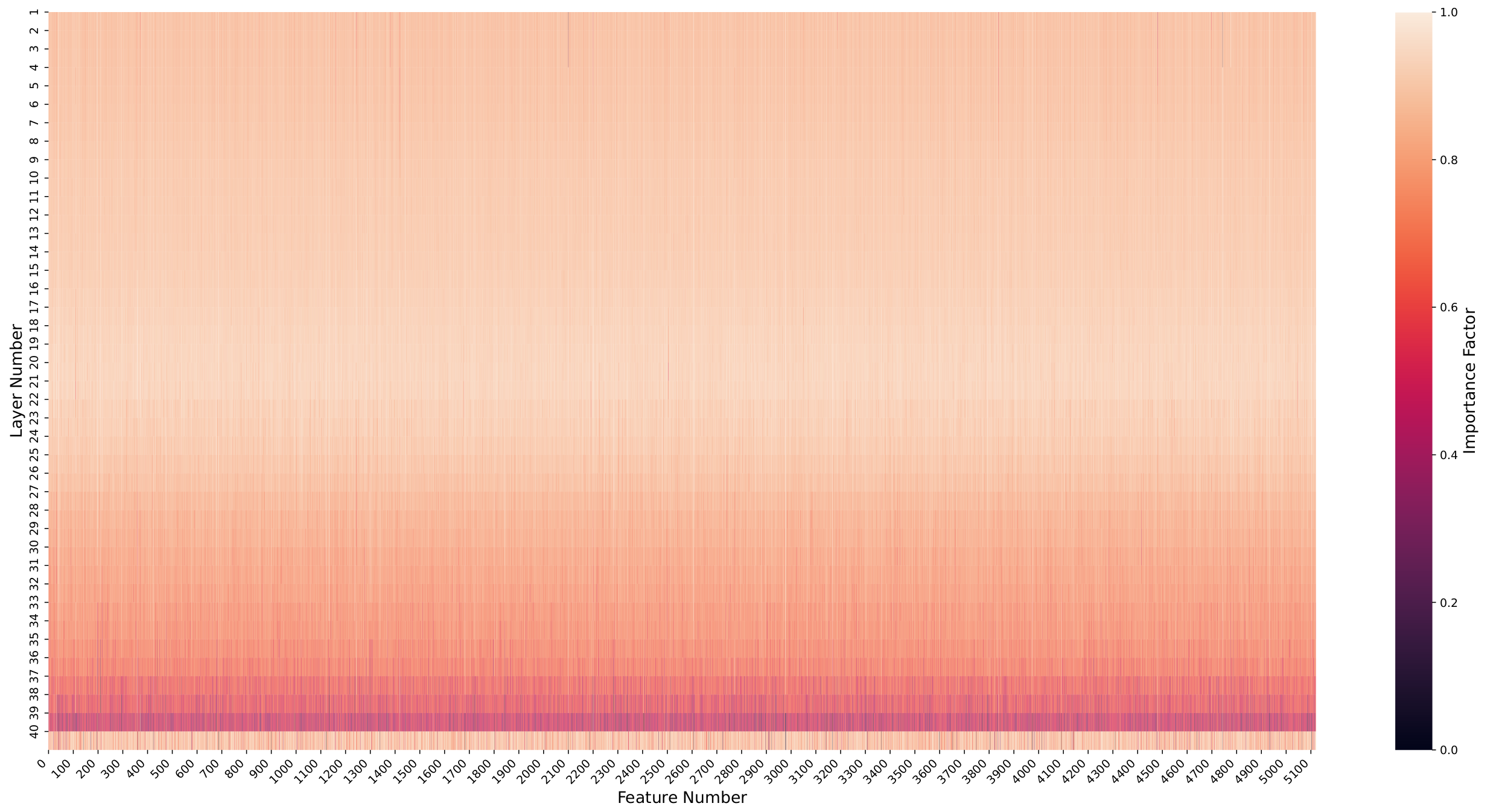
Text interpretation: This pattern indicates a balanced hierarchical feature extraction approach, with both lower and higher-level features playing a significant role, particularly those extracted by the early to middle layers.
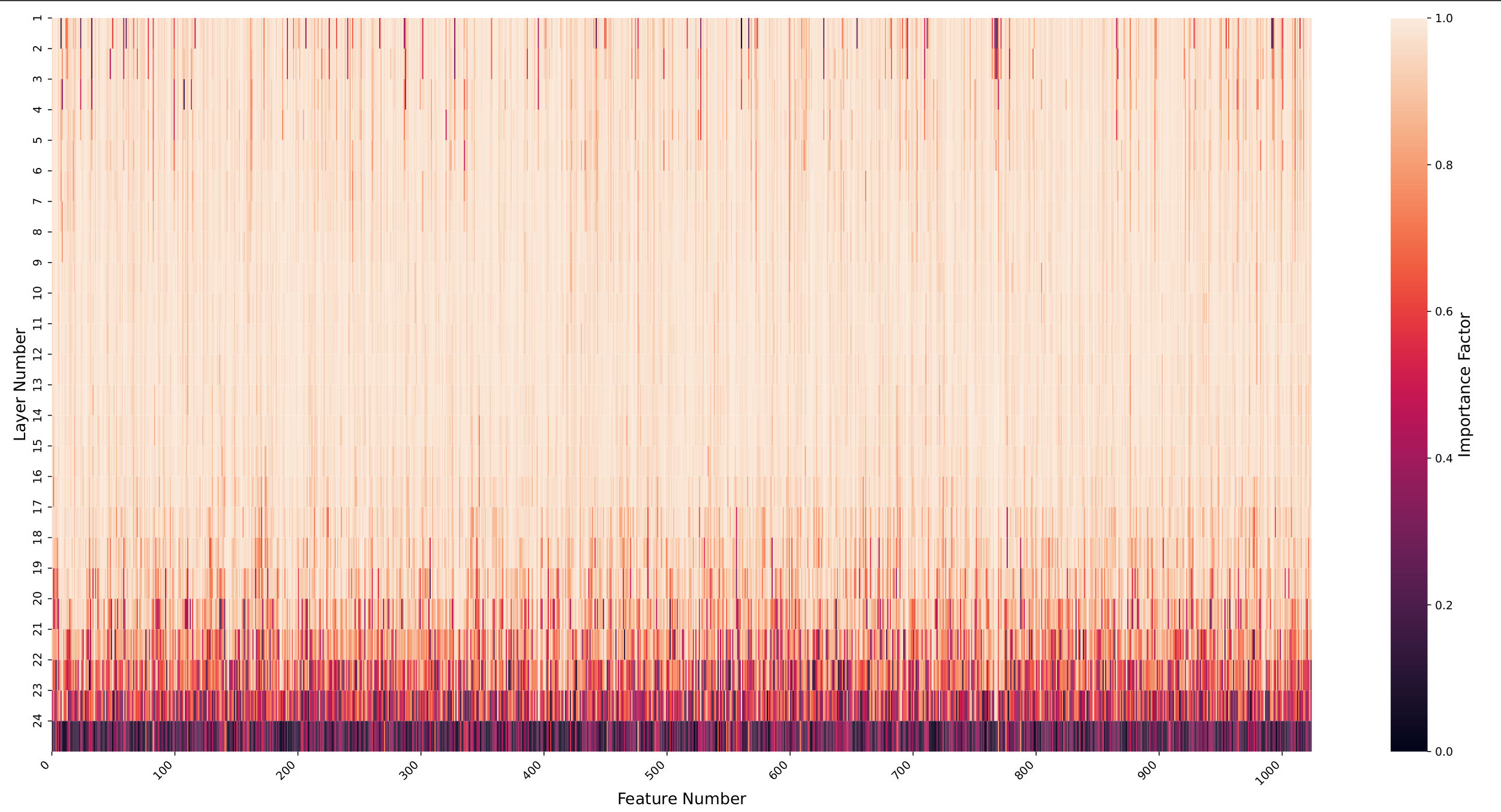
Vision interpretation: This reflects the necessity of early-stage feature extraction in visual tasks, such as identifying edges and textures.
These variations in IF value distribution underscore the distinct information processing requirements of each modality. Speech and image processing appear to rely on primary feature extraction, while text processing demands both fundamental and complex feature identification. The insights provided by IF analysis enhance the explainability of the models, offering a quantifiable measure of feature significance.
Layer Contribution Analysis
Analysis of the layer contribution indicates earlier layers exhibit more meaningful features and contribute more to model performance, suggesting potential overparameterization in later layers
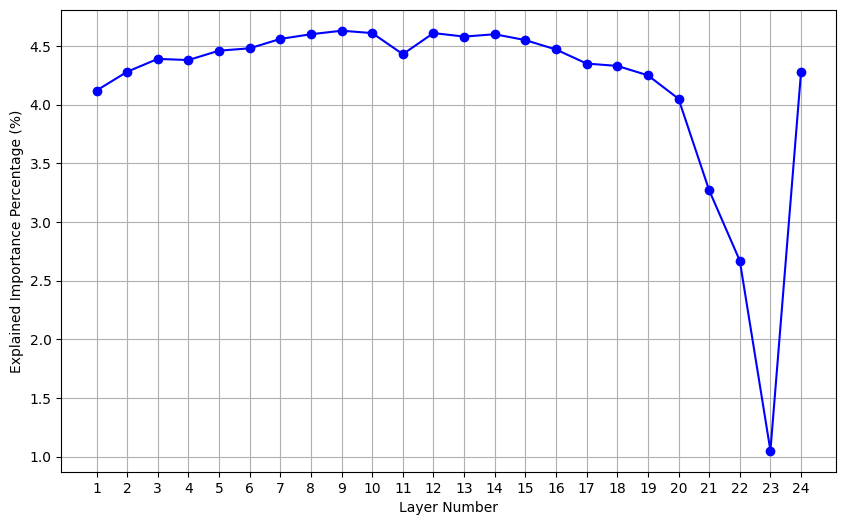
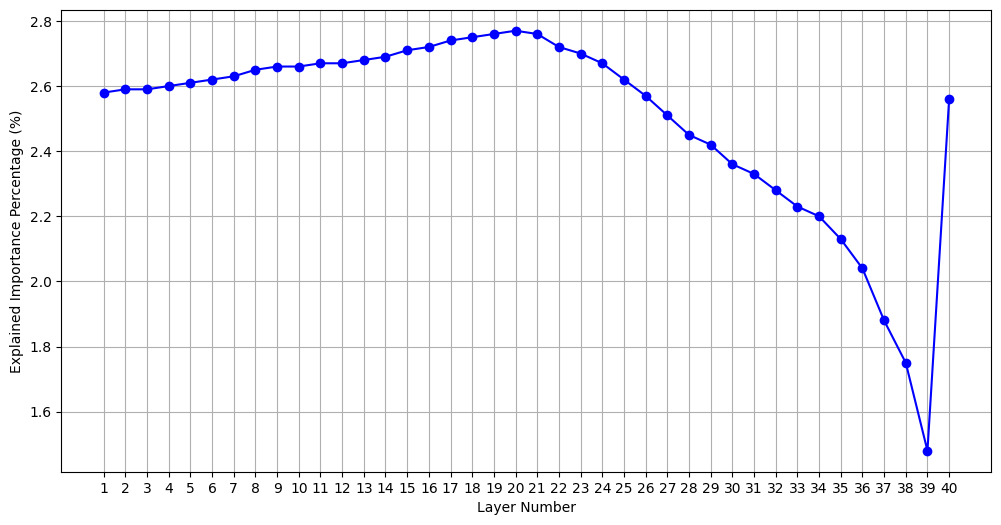
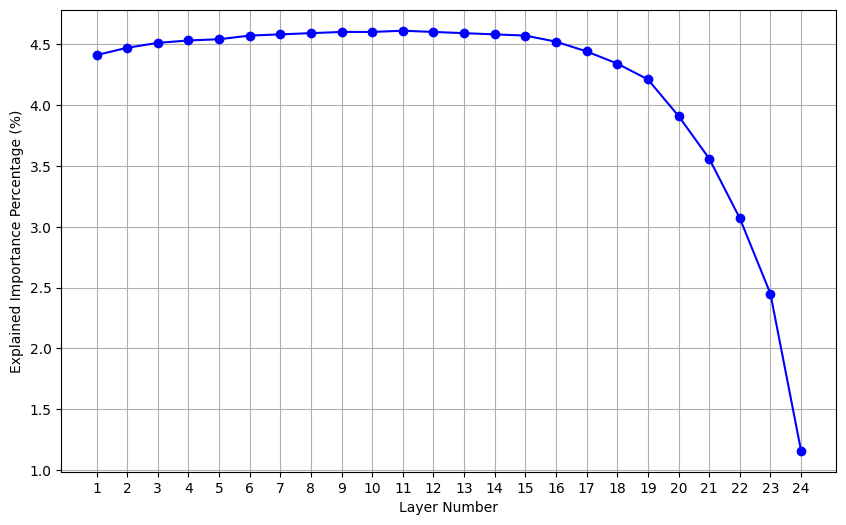
Validating the Importance Factor: Ablation Studies
To rigorously validate that IF scores from DAAM accurately identify key feature extraction regions, we conduct systematic ablation experiments. We retrain models using only layers with high IF scores versus only layers with low IF scores, then compare performance.
Hypothesis: If IF truly measures layer importance, then high-IF layers should significantly outperform low-IF layers.
Speech: IEMOCAP Layer Ablation
| Layer Selection | F1 | F2 | F3 | F4 | F5 | Average | Std Dev |
|---|---|---|---|---|---|---|---|
| Layer 9 (High IF) | 65.9 | 60.1 | 64.4 | 62.7 | 67.0 | 64.0 | 2.40 |
| Layer 23 (Low IF) | 62.8 | 58.9 | 63.2 | 62.0 | 64.5 | 62.3 | 1.89 |
| Performance Difference | +1.7% | ||||||
Key Finding: Layer 9 (high IF score) achieves +1.7% absolute improvement over Layer 23 (low IF score), validating that IF scores correlate with actual layer importance for the downstream task.
Vision and Text: Multi-Layer Ablation
| Dataset | Model | High IF Layers | Accuracy | Low IF Layers | Accuracy | Difference |
|---|---|---|---|---|---|---|
| AG News | Llama2-13B | Layers 19-21 | 94.9% | Layers 37-39 | 94.7% | +0.2% |
| CIFAR-100 | BEiT-Large | Layers 10-12 | 72.6% | Layers 22-24 | 64.7% | +7.9% |
Key Findings:
- Text processing: Modest but consistent gain (+0.2%), reflecting the distributed nature of linguistic feature extraction
- Vision processing: Dramatic gain (+7.9%), demonstrating that early layers (10-12) capturing low-level features are critical for image classification
Why IF is Superior to Traditional Attention Weights
Critical Distinction: Correlation vs. Importance
In standard Multi-Head Attention (MHA), attention weights indicate the level of correlation
Case Study: The Layer 23 Paradox
Previous work
But our ablation study reveals:
- Layer 23 (identified as “important” by MHA): 62.3% accuracy
- Layer 9 (identified as “important” by DAAM IF): 64.0% accuracy
Why the discrepancy?
- MHA attention weights measure inter-layer correlation:
- High attention weights → strong relationships between tokens
- Does NOT mean these relationships help the downstream task
- Can identify layers that are “active” but not “useful”
- DAAM’s IF measures task-aligned importance:
- High IF scores → features that improve classification
- Directly optimized for the end goal during training
- Identifies layers whose features actually matter for performance
Implications:
- For model interpretability: IF provides more actionable insights than MHA attention weights
- For architecture optimization: IF can guide layer pruning and model compression
- For transfer learning: IF helps identify which layers to fine-tune vs. freeze
Cross-Modal Patterns in Layer Importance
Across all three modalities, we observe consistent patterns:
Speech (WavLM):
- High IF concentration in lower layers (especially layer 9)
- Suggests fundamental acoustic features captured early are most predictive
- Upper layers refine but don’t add as much discriminative power
Text (Llama2):
- More uniform IF distribution across layers with slight emphasis on early-to-middle (19-21)
- Reflects hierarchical feature extraction: both low-level (syntax) and high-level (semantics) matter
- Balanced importance across the network
Vision (BEiT):
- Strong emphasis on lower layers (10-12)
- Early-stage features (edges, textures, colors) are critical for classification
- Aligns with visual processing theory: low-level features compose high-level representations
Practical Applications of IF
The validated IF metric enables several practical applications:
- Efficient Fine-Tuning: Focus adaptation on high-IF layers only
- Interpretability: Understand which encoder layers contribute to decisions
Example: Analysis of Figure 3a-c (layer contribution) indicates earlier layers contribute more to model performance, suggesting potential overparameterization in later layers
Advanced Applications
Vector Quantized Variational Autoencoder (VQ-VAE)
To demonstrate the applicability of DAAM in more complex architectures, the paper integrates the proposed attention mechanism into a Vector Quantized Variational Autoencoder (VQ-VAE). This application represents a significantly more challenging use case than the classification tasks presented in the main paper.
Architecture:
The DAAM-enhanced VQ-VAE architecture consists of:
Encoder: Initial convolution followed by a series of downsampling blocks. Each DownSampleBlock consists of strided convolution (stride=2) for downsampling, Group normalization, ReLU activation, and a DAAM-enhanced residual block that applies Multi-Head Density Adaptive Attention on the channel dimension.
Vector Quantizer: Maps continuous encodings to nearest vectors in a learned discrete codebook containing num_embeddings vectors of embedding_dim dimensions.
Decoder: Initial convolution followed by a series of upsampling blocks. Each UpSampleBlock consists of transposed convolution (stride=2) for upsampling, Group normalization, ReLU activation, and a DAAM-enhanced residual block with Multi-Head Density Adaptive Attention.
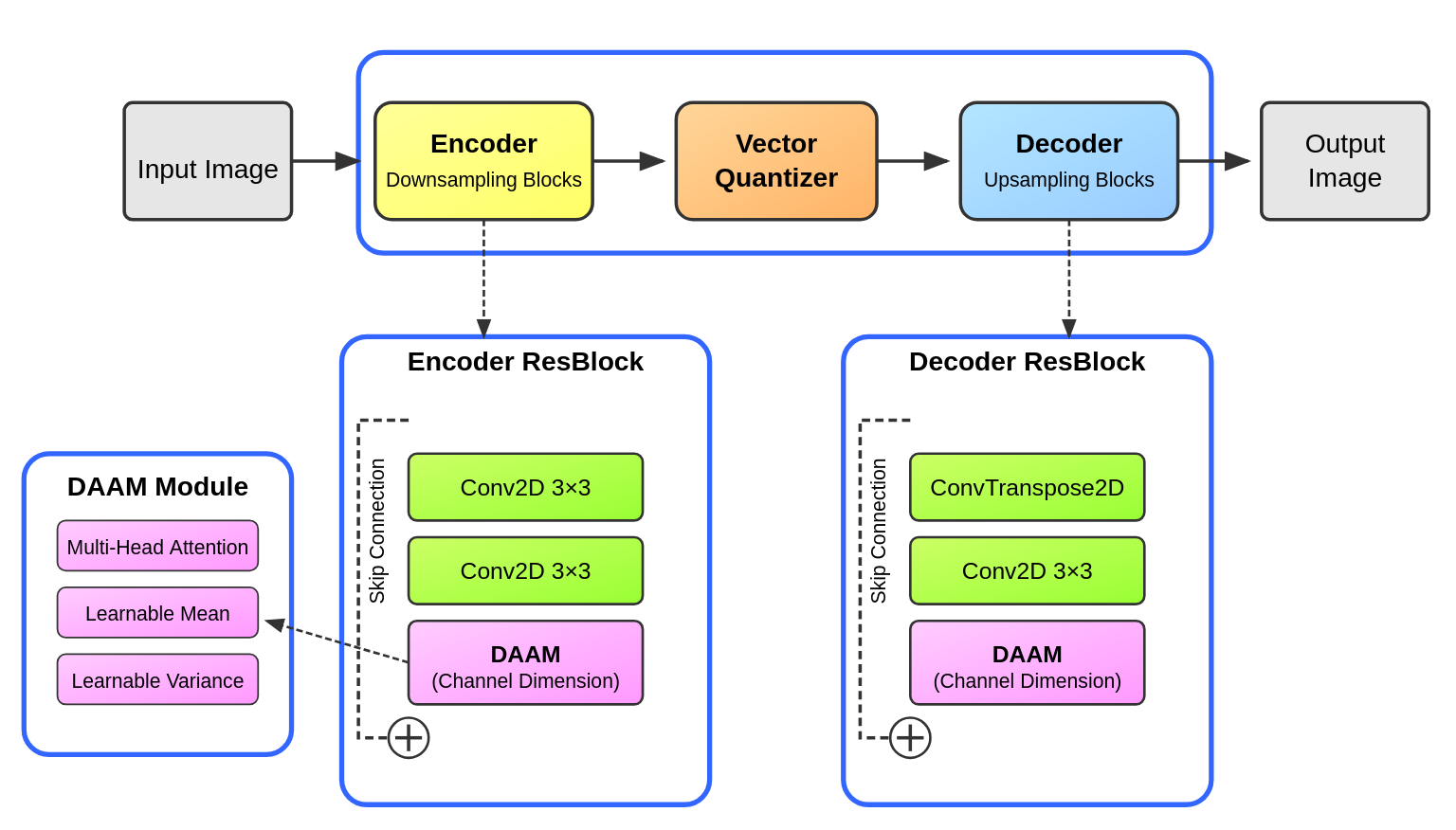
This architecture applies DAAM along the channel dimension (norm_axis=1), which is particularly effective for enhancing feature representation in the bottleneck of the VQ-VAE.
Training details:
- Hidden dimensions: [128, 256, 512]
- Latent dimension: 256
- Codebook size: 1024 embeddings
- Image size: 256×256
- DAAM configuration: 4 heads with 3 Gaussians per head
- Optimizer: Adam
, lr=3e-4 - Epochs: 176
- Batch size: 32
- Dataset: COCO-2017

The integration of DAAM substantially improves reconstruction quality, particularly for fine details and textures that are challenging for standard VQ-VAE models. The DAAM mechanism proves particularly effective at addressing common VQ-VAE failure modes such as blurriness and loss of texture details. By dynamically adjusting attention across channels based on input content, the model preserves more perceptually important features.
This application demonstrates DAAM’s versatility beyond classification tasks, showcasing its effectiveness in generative modeling contexts where adaptive feature selection is crucial for high-quality outputs.
Mixture of Densities Extension (DAAMv2)
The paper presents an extension of the Multi-Head Density Adaptive Attention Mechanism (DAAM), focusing on enhancing the stability of the training process and the model’s efficiency by significantly reducing the number of learnable parameters even further.
Algorithm:
Algorithm: Mixture of Densities Adaptive Attention
Input: x (input tensor), normAxis, N Gaussians, eps
Output: Attention-modified x
1. Initialize m, c of size N
μ ← mean(x, axis=normAxis)
σ² ← var(x, axis=normAxis) + eps
mixture ← 1
2. For i = 0 to N-1:
μᵢᵃᵈʲ ← μ + m[i]
yᵢ ← (x - μᵢᵃᵈʲ) / √(σ²)
gᵢ ← exp(-yᵢ²/(2·c[i]²)) / √(2π·c[i]²)
mixture ← mixture · gᵢ
3. Normalize mixture across normAxis
4. x' ← x · mixture
5. Return x'
The extended DAAM incorporates multiple attention heads, each with its Gaussian mixture model, to process different segments of the input tensor in parallel. Additionally, the algorithm adds the original input features to the augmented one for enhanced stability during training (i.e., X’ ← X’ + X).
Extended Results:
| Dataset | Method | Results |
|---|---|---|
| IEMOCAP | Mixture of DAAM | 67.9 ± 1.35 |
| CIFAR-100 | Mixture of DAAM | 80.3 ± 0.30 |
| AG News | Mixture of DAAM | 94.6 ± 0.05 |
It is evident that Mixture of DAAM not only outperforms DAAM but it also reduces its overall trainable parameter count significantly. With only 64 parameters (8 heads × 4 Gaussians × 2 params), this achieves substantial parameter reduction.
Limitations and Future Work
The paper acknowledges the following limitations:
Fixed number of Gaussians: The Density Adaptive Attention mechanism’s fixed number of Gaussians can limit its adaptability across different datasets and tasks.
Proposed improvements:
- Implementing Bayesian approaches with Bayesian Information Criterion for dynamic Gaussian selection
- Exploring DAAM in more diverse tasks, datasets, and grounding experiments
- Model compression via attention weights during training—particularly valuable for resource-constrained applications
Conclusion
This work introduces the Multi-Head Density Adaptive Attention Mechanism and the Density Adaptive Transformer, demonstrating their effectiveness in enhancing model performance, particularly with highly non-stationary data. Results show that combining learnable mean and variance for multiple Gaussian Distributions enables dynamic feature significance recalibration and approximation of any Probability Distribution across multiple modalities.
Key contributions:
- DAAM with fully learnable Gaussian parameters enabling dynamic recalibration of feature importance
- Introduction of the Importance Factor for improved model explainability
- Comprehensive validation across Speech, Text, and Vision modalities
- Integration with Grouped Query Attention with minimal parameter increase (0.016%-0.08% compared to GQA models) and 80% fewer parameters than LoRA
Results summary:
| Modality | Dataset | Baseline | Best DAAM | Improvement |
|---|---|---|---|---|
| Speech | IEMOCAP | 62.3% | 67.4% | +5.1% |
| Vision | CIFAR-100 | 61.7% | 80.6% | +18.9% |
| Text | AG News | 94.6% | 94.9% | +0.3% |
Overall, DAAM represents an advancement towards development of better performing and more explainable attention models across multiple modalities.
Acknowledgments
We thank the creators of WavLM, Llama, and BEiT for releasing their pre-trained models. We are grateful for the IEMOCAP, Librilight, AG News, CIFAR-100, and COCO datasets that enabled this research.
Code Availability
The complete implementation is available on GitHub: https://github.com/gioannides/DAAM-paper-code
Source code has also been uploaded in the supplementary material section.